Consider the total orders \(P = Q = \underline{3}\) with the following monotone maps:
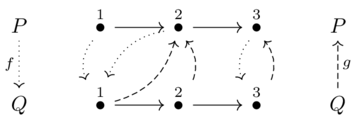
These do form a Galois connection
These maps do not form a Galois connection:
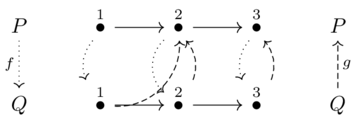
These do not because of \(p=2, q = 1\)
\(f(p)=2 \not \leq q=1\) which is not the same as \(p = 1 \leq g(q)=2\)
In some sense that can be formalized, for total orders the notion of Galois connection corresponds to the maps not ‘crossing over’.